В сложных прикладных решениях 1С:Предприятия существует прикладной функционал расчета себестоимости товаров. Это достаточно сложная задача и 1С решила сделать встроенный в платформу механизм, который будет максимально простым в использовании и, при этом, весьма производительным.
Проанализировав работу прикладных решений, 1С пришла к выводу, что один из наиболее трудозатратных этапов представляет собой, по сути, решение системы линейных алгебраических уравнений (СЛУ). В результате в платформе, во встроенном языке, 1Среализовали новый объект, позволяющий находить решение СЛУ.
Существуют классические алгоритмы решения СЛУ, однако в платформе 1С использовала собственный алгоритм с дополнительной оптимизацией. В случае разреженной матрицы СЛУ, что как раз соответствует задаче расчета себестоимости, наш алгоритм работает существенно быстрее классических алгоритмов. В случае плотной матрицы СЛУ он показывает результаты, близкие к классическим (гарантированно не хуже).
По нашим оценкам использование этого нового объекта в задаче расчета себестоимости позволит увеличить производительность в десятки раз.
Помимо этой задачи вы можете использовать новый объект и в других прикладных областях, которые автоматизируются решениями 1С:Предприятия:
- Задачи планирования;
- Взаиморасчеты между некоторым множеством юридических лиц, предприятий или отраслей;
- Балансовые модели;
- Прогнозирование;
- Задачи поиска экстремумов, в том числе условных экстремумов.
Задача решения системы линейных алгебраических уравнений
В общем виде система линейных алгебраических уравнений выглядит следующим образом:
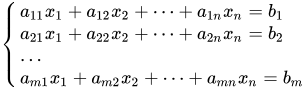
где ![]() это известные коэффициенты уравнений.
это известные коэффициенты уравнений.
Решение системы линейных уравнений заключается в нахождении таких значений ![]() , при которых все равенства выполняются.
, при которых все равенства выполняются.
Новый объект РасчетСистемЛинейныхУравнений
Объект РасчетСистемЛинейныхУравнений обладает рядом свойств, которые позволяют гибко настраивать необходимую точность решения через численные значения и количество итераций алгоритма. Кроме этого они позволяют устанавливать границу изменения алгоритма решения для получения оптимальной скорости вычислений.
Объект содержит конструктор и два метода:
- РассчитатьСистемыЛинейныхУравнений() - решает систему линейных уравнений и возвращает решение в виде объекта ТаблицаЗначений;
- ПолучитьКомпонентыСвязности() - находит компоненты связности и возвращает результат в виде объекта ТаблицаЗначений. Вы можете использовать этот метод для выделения нескольких подмножеств данных и распределённой работы с ними.
Особенностью нового функционала является то, что он поддерживает параллельное использование вычислительных ресурсов. Вы можете регулировать количество используемых потоков вычисления. Функционал доступен на сервере, в толстом клиенте и в COM-соединении.
Схема использования механизма
Для решения системы линейных уравнений необходимо подготовить две таблицы с коэффициентами системы линейных уравнений – ИсточникДанныхУзлов и ИсточникДанныхСвязей. Эти таблицы могут быть объектами типа ТаблицаЗначений или РезультатЗапроса.
- ИсточникДанныхУзлов - должен содержать колонку с номерами уравнений и множество колонок, хранящих свободные коэффициенты уравнений;
- ИсточникДанныхСвязей - так же содержит колонку с номерами уравнений, колонку номеров переменных и множество колонок, хранящих коэффициенты, с которыми переменные входят в уравнения.
Далее нужно дать описание этих таблиц, выставив определенные свойства объекта РасчетСистемЛинейныхУравнений: КолонкаУравненияВУзлах, КолонкаУравненияВСвязях, КолонкаПеременныеВСвязях.
Следующим шагом является описание систем линейных уравнений, которые требуется решить. Для этого существует специальный объект ОписаниеСистемыЛинейныхУравнений. В нем нужно указать свойства КолонкаКоэффициентовВСвязях и КолонкаКоэффициентовВУзлах, соответствующие данной системе.
Полученные описания следует добавить в коллекцию ОписанияСистемЛинейныхУравнений (свойство ОписанияСистем объекта РасчетСистемЛинейныхУравнений). Для корректной работы нужно добавить в коллекцию как минимум одно ОписаниеСистемыЛинейныхУравнений.
Далее можно указать дополнительные (необязательные) свойства объекта РасчетСистемЛинейныхУравнений, которые позволяют тонко настроить механизм решения.
Финальный этап - вызов метода РассчитатьСистемыЛинейныхУравнений().
Отметим, что механизм позволяет рассчитывать сразу несколько систем линейных уравнений за один вызов метода РассчитатьСистемыЛинейныхУравнений().